Aspherical surface equation.
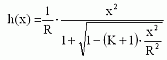
These web pages are a slightly updated revival of the original KOJAC web pages, that don’t exist anymore on the web site of the Applied Optics Group of IMT (formerly at the University of Neuchâtel, now at EPFL).
Aspherical lenses are not widely used in optics because of their high cost, but they are sometimes required because of their capacity to reduce aberrations. In modern optics, it becomes more and more easy to manufacture them, especially by injection moulding processes. These surfaces are ususally described by the profile h(x) given by,
Aspherical surface equation.
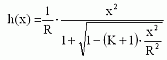
with x representing the lateral position variable, R the radius of curvature at the vertex (i.e. the inverse of the curvature C) and K the conic coefficient. The significance of K is:
Correspondance between K and the type of profile.
| Value of K | Type of profile |
|---|---|
| > 0 | ellipse |
| = 0 | sphere |
| -1 < < 0 | ellipse |
| = -1 | parabola |
| < -1 | hyperbola |
This tutorial shows the refraction of a parallel bundle of light rays at an interface whose profile is described by the previous equation. You can act on both the light rays and the interface.
You can change the light beam direction and - through an aperture whose size and position are variable - modify the beam size. An interesting property to observe is the appearance of the caustic, the envelope curve of the beam, as shown in the example below.
Observation of the caustic.

Notice moreover that the rays that degrade the quality of the lens effect are the marginal rays, especially the ones that fall upon the interface with an angle far from normal incidence.
The applet also allows the modification of the surface parameters, namely the curvature C = 1/R , the conic coefficient K and the refraction indexes before and after the interface.
This aspherical surface exhibits an interesting property: if the Conic coefficient is the square of the refraction indexes ratio (times -1), then the on axis aberrations are suppressed. The starting position of K = -2.25 for n1 = 1.5; n2 =1.0 presents this property.
Unfortunately, this property is only valid on-axis, which can be experimented here. This explains why aspherical lenses are for very specific uses only.